Just intonation (hereinafter “JI”) is any system of tuning in which all of the intervals can be represented by ratios of whole numbers, with a strongly implied preference for the smallest numbers compatible with a given musical purpose. Unfortunately, this definition, while accurate, doesn't convey much to those who aren't already familiar with the art and science of tuning. The aesthetic experience of just intervals and chords, however, is unmistakable.

The simple-ratio intervals upon which JI is based are what the human auditory system recognizes as consonance, if it ever has the opportunity to hear them in a musical context.¹ The significance of whole-number ratios has been recognized by musicians around the world for at least 2,500 years.

JI is not a particular scale, nor is it tied to any particular musical style. It is, rather, a set of principles that can be used to create a virtually infinite variety of intervals, scales, and chords that are applicable to any style of tonal music (or even, if you wish, to atonal styles). JI is not, however, simply a tool for improving the consonance of existing music; It is a gateway to a new and expanded palette of musical intervals and subtle distinctions hitherto unknown to Western composers. Ultimately, it is a method for understanding and navigating through the boundless reaches of the pitch continuum—a method that transcends the musical practices of any particular culture.

In order to understand what “simple-ratio intervals” are and why they are musically significant, we must first examine some concepts of acoustics and psychoacoustics. When we speak of musical intervals, we are describing relations of pitch, a perceptual phenomenon, which is closely correlated with frequency, a physical phenomenon. Sounds that have definite pitch, i.e., those to which we can assign note names such as A, Bb, C#, and so on, correspond to periodic vibrations, waveforms that repeat at regular time intervals. A musical interval is a relation between two pitches, and hence, a relation between two periodic vibrations, which can be represented by numbers. Frequencies are measured in Hertz (abbreviated Hz), where 1Hz = one cycle per second.

Periodic vibrations may be simple or pure tones (sine waves) but the tones of most musical instruments are composed of a number of simple tones (partials) that are whole-number multiples of the fundamental frequency of the tone (the lowest frequency component and the one that normally corresponds to the perceived pitch). This series of whole number multiples² is known as the harmonic series. In other words, the harmonic series is the series of all integer (positive whole-number) multiples of some frequency f (f, 2f, 3f, 4f, 5f, …). Hence, the relationship between any two members of the series is an integer ratio. Figure 1 illustrates the first sixteen members of the series on the pitch C2, but what is significant is the pattern of intervals between the successive tones of the series, rather than the specific pitches of the series. Although the series is represented here in a variant of conventional staff notation, all of the intervals of the series, except the octave, deviate significantly from those of the equally tempered scale (or to put things in a more proper order, the intervals of the tempered scale deviate from those of the harmonic series). The precise deviations, expressed in cents, where 1 cent = 1/100 equal semitone or 1/1200 octave, are given in Table 1

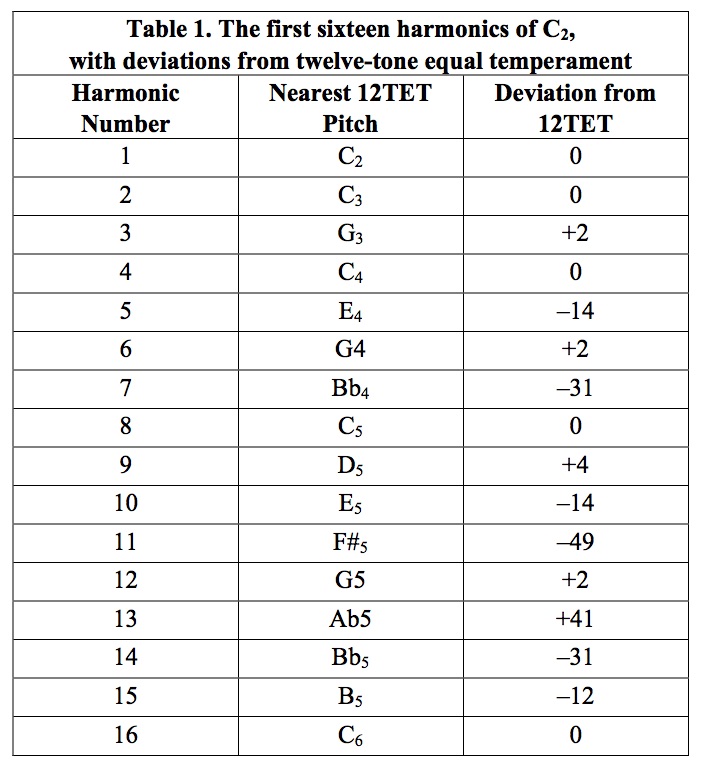
When the human auditory system encounters a group of pure tones with relative frequencies that correspond to low-numbered degrees of a harmonic series sounding simultaneously, it does not normally hear several separate tones with distinct pitches. Rather, it hears a single entity. This entity is perceived as a tone with a pitch corresponding to the repetition rate of the composite wave, which corresponds to that of the fundamental of the series. It is not necessary for the fundamental or one of its octave multiples to be among those tones actually being sounded for this response to occur, nor is it necessary for other conflicting tones to be absent. As few as two or three relatively low-numbered members of the series are sufficient to produce the sensation that the fundamental is being heard. The reason our auditory system is specially equipped to recognize the harmonic series should be obvious: All sustained, pitched sounds produced by the human voice consist of a portion of a harmonic series, with certain portions of the harmonic spectrum receiving a characteristic emphasis. The human auditory system is, of course, highly specialized for the recognition of human speech.

Although the harmonic series, like the series of integers, is theoretically infinite, the series of partials making up any complex musical tone is finite. The number of partials present in a given tone, their relative intensities, and the way their intensities vary over time are the primary determinants of the musical property known as timbre or tone color. The relative intensities of the different partials making up a given complex tone are referred to as the harmonic spectrum of that tone. As will be explained below, harmonic partials have a significant effect on the consonance of musical intervals, so the presence or absence of a particular partial in the spectrum of a given instrument will have an effect on the quality of certain intervals played on that instrument.

The aspect of relationships between simultaneously sounded complex tones that has attracted the most attention among theorists is the coincidence of certain harmonics when pairs of complex tones are tuned in simple-ratio intervals, or conversely, the presence of beats resulting from the non-coincidence of these same partials when pairs of complex tones deviate from these simple intervals.

Beats take place between two simple tones whose frequencies are near unison. These beats—regular variations in loudness—occur at a rate that is the difference in Hz between the two generating frequencies. Beats can be perceived clearly when the difference is less than 20–25Hz, but as the difference increases beyond this point the beats blend together, giving rise to a general sensation of roughness. This roughness gradually decreases as the difference increases, persisting until the difference exceeds an interval called the critical band, which, for most of the audio range, falls between a whole tone and a minor third.

Beating will occur between the partials of complex tones when they fall in the near-unison range, as described above. When two complex tones with harmonic partials form a whole-number ratio interval, the numbers of the ratio indicate the lowest pair of harmonics that will match between the two tones. For any integer ratio of the form m:n, where m represents the higher tone, the mth harmonic of the lower tone, and the nth harmonic of the higher tone will coincide. For example, in the case of the perfect fifth (ratio 3:2), the third harmonic of the lower tone matches the second harmonic of the higher tone. In the case of the perfect fourth, (ratio 4:3) the fourth harmonic of the lower tone matches the third harmonic of the higher tone. Higher harmonics that are integer multiples of the lowest matching pair will, of course, also match, for example, in the case of the perfect fifth, 6:4, 9:6, 12:8, etc. The simple-ratio forms of several of the principal consonances with their matching harmonics are illustrated in Figure 2. (The matching harmonics are represented by triangular noteheads joined by dotted horizontal lines.) In intervals that deviate from these simple-ratio forms, the mismatched harmonics form mistuned unisons, and beats are generated at a frequency corresponding to the difference between the frequencies of the harmonics in question. This fact provides an essential cue for tuning any of these simple consonances by ear on instruments producing harmonic or nearly harmonic partials. One simply listens for and eliminates the beats between the defining pair of harmonics.

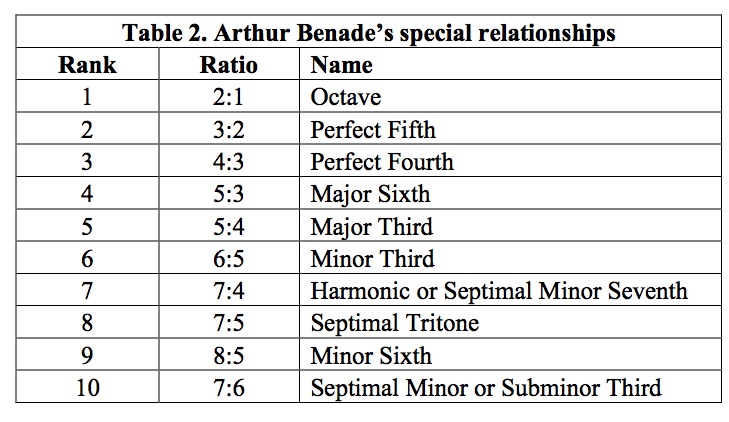
n his excellent book, The Fundamentals of Musical Acoustics³, physicist and flutist Arthur H. Benade describes an experiment that he frequently performed with his students, which gives an accurate picture of the role played by beats as cues for tuning simple-ratio intervals between sustained tones with harmonic partials. Benade used two audio oscillators that were constructed so as to produce tones with three or four exactly harmonic partials of appreciable strength. One oscillator is tuned to a fixed frequency somewhere in the range of 250–1,000Hz (C4–C6). A volunteer is then invited to tune the second oscillator up or down until he or she finds a setting that produces a “special relationship,” which Benade describes as “a beat-free setting, narrowly confined between two restricted regions in which a wide variety of beats take place.” According to Benade, experiments of this type consistently identified as special relationships those intervals listed in Table 2. As those who are familiar with theories of JI will recognize, the intervals in the table are precisely those that are almost universally regarded as consonances by advocates of JI. It is particularly notable that, in addition to intervals commonly regarded as consonances (albeit in their tempered versions) by conventional music theory, the table includes three ratios involving seven (7:4, 7:5, and 7:6) that are not recognized in conventional music theory. Indeed, 7:4 is in the vicinity of the tempered minor seventh (1,000 cents) and 7:5 is even closer to the tempered tritone (600 cents), both intervals that conventional theory identifies as dissonances. It is apparent, therefore, that the experimenters are not simply picking out intervals that are familiar as consonances from their musical training but are really responding to the special physical properties of these particular whole-number ratio intervals.

Equally revealing is the reaction Benade got from his students when he retuned the variable oscillator from one of the special integer relationships to a nearby tempered interval normally accepted as a consonance. When, for example, he substituted the tempered major third (400 cents, approximately 1.25992:1) for the just 5:4, all of the musicians in the room agreed that the interval was “an out of tune (sharp) major third.” His listeners “typically react with skepticism or dismay” when they are told that the out-of-tune interval they are hearing is a correctly tuned major third from the perspective of the culturally dominant system. “What,” they ask, “makes anyone think that those are acceptable tunings?”

In addition to the absence of beating partials, there are other phenomena that distinguish simple-ratio intervals from all others. When two or more tones are sounded simultaneously with sufficient intensity, the nonlinear response of the ear may generate additional tones that are musically significant. These tones are known variously as combination tones, resultant tones, summation tones and difference tones, or intermodulation products. The most commonly heard of these tones is that known as the primary or first-order difference tone. For two tones with frequencies f1 and f2, the frequency of the first-order difference tone is (f2 – f1), where f2 is the higher frequency. Difference tones with the frequencies 2f1 – f2 or 3f1 – 2f2 may also sometimes be detected. Figure 3 illustrates the difference tones generated by the most important simple-ratio intervals. In every case, the difference tones correspond to lower degrees of a harmonic series to which the parent tones belong. In a sense, the difference tones identify the intervals as belonging to larger tonal sets. For example, the major third 5:4 (between middle C and E in the figure) generates as difference tones two Cs and a G, implying a strong C Major tonality.

A third phenomenon, known variously as periodicity pitch, virtual pitch, subjective pitch, residue tone, or the missing fundamental, also reinforces the harmonic series identities of simple-ratio intervals. Unlike difference tones, which are produced by nonlinear responses in the middle and inner ear, periodicity pitch appears to be the result of higher-level neural processes. In many cases, the periodicity pitch of an interval is the same as its first-order difference tone. (Figure 4).

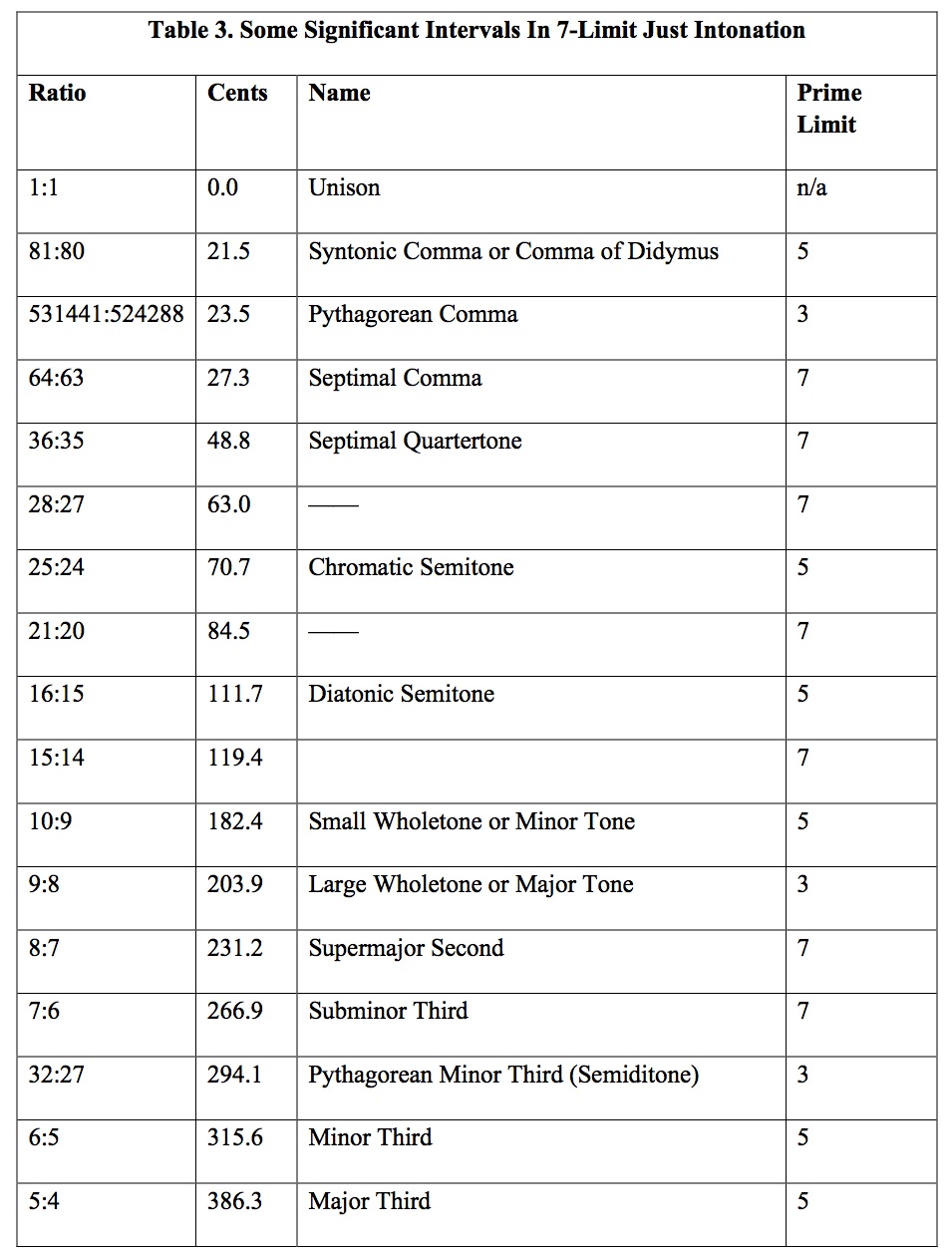
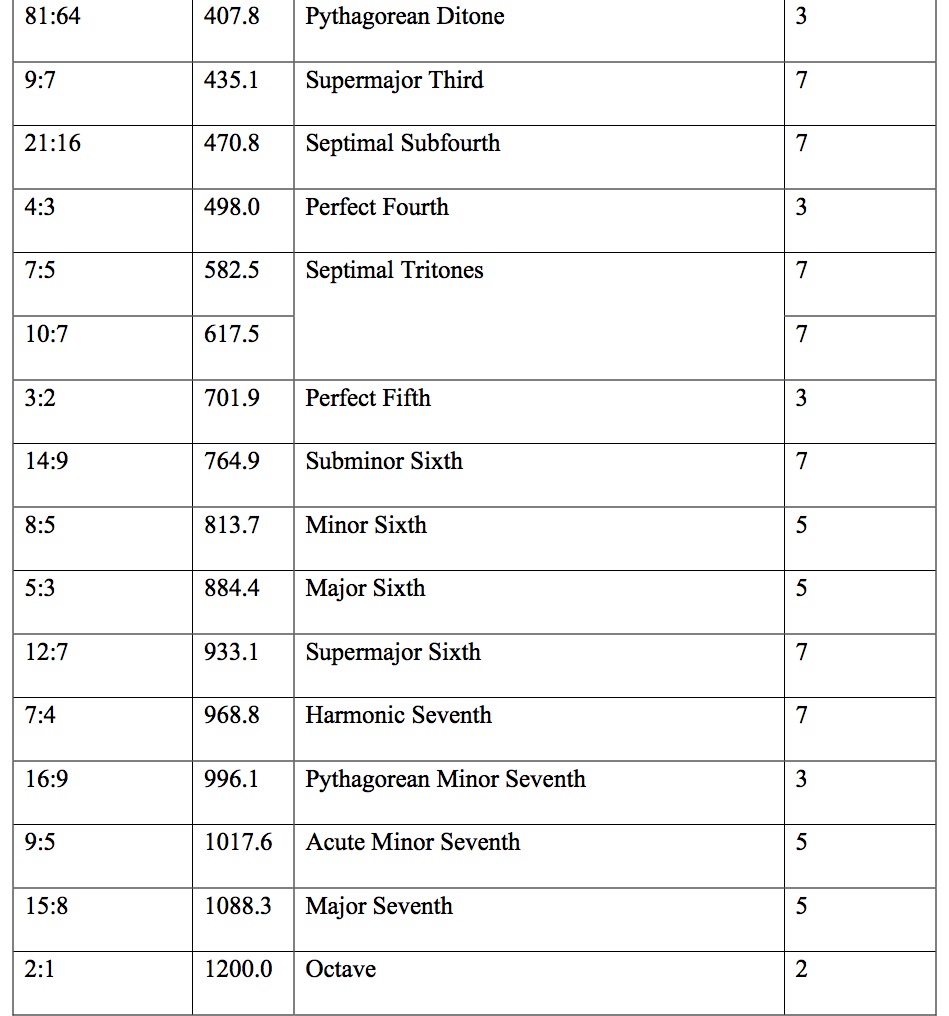
The combination of the three properties just described, absence of beating harmonics and harmonically related difference tones and periodicity pitches, distinguish this small set of simple-ratio intervals from all other possible musical relationships. Although each interval is unique in its effect, all share common properties of clarity, purity, smoothness, and stability; these properties make them the foundation of JI. This is not to say that they are the only musically useful intervals in JI. On the contrary, adding, subtracting, and recombining these intervals in various combinations gives rise to large families of intervals that are essential for the construction of scales and melodic lines. A selection of significant intervals in 7-limit JI is shown in Table 3.

How do the intervals of twelve-tone equal temperament (12TET), the predominant tuning system in the West over the past 250+ years, compare with the simple-ratio intervals I just described? The basic premise of temperament (any temperament) is that the number of pitches required to play in different keys can be reduced by compromising the tuning of certain tones so that they can perform different functions in different keys, whereas in JI a slightly different pitch would be required to perform each function. In other words, temperament compromises the quality of intervals and chords in the interest of simplifying instrument design and construction and playing technique. 12TET takes advantage of the fact that the sum of twelve perfect fifths (312:212) is slightly greater than seven octaves (27:1). The difference is the Pythagorean comma (531,441:524,288, about 23.5 cents). Each fifth in 12TET is flatted (narrowed) by 1/12 of the Pythagorean comma (approximately 1.96 cents) causing the fifths to form a closed circle. To achieve this, the starting frequency is multiplied twelve times in succession by the twelfth root of two (12√2), an irrational number that is approximately 1.05946. This ensures that none of the resulting intervals except the octave will be simple ratios. The problems with 12TET are not limited to its fifths being slightly narrow; chaining fifths, whether perfect or slightly flatted, does not result in good thirds or sixths. And, of course, 12TET, being a closed system, makes no provision for the admission or understanding of any additional intervals. It provides “acceptable” approximations of those intervals that most musicians in Europe c. 1750 considered useful and no more. Attempts by some twentieth-century composers and musicians to expand the resources of 12TET by subdividing it into smaller arbitrary intervals, such as quarter tones, third tones, etc., failed to solve its fundamental psychoacoustic problems.

Let us examine a few of the intervals of 12TET. As expected, the 12TET perfect fifth is not bad. In the case of the fifth between middle C and the G above, the third harmonic of the C and the second harmonic of the G beat at less than 1Hz (before the advent of electronic tuners, the standard method for tuning a piano in 12TET was to count the beats of the fifths with a stopwatch). The first and second order difference tones, (f2 – f1) and (2f1 – f2) are each less than one cent away from the C below middle C. The third order difference tone is below the range of human hearing. The case of the perfect fourth is similar. If one wanted to make music in which only fifths, fourths, and octaves were consonant, 12TET would be adequate. The 12TET major third fares much worse. At 400 cents, it is 13.68 cents wider than the just 5:4. In the case of the major third between middle C (261.6Hz) and the nearest E above it (329.6Hz), the fifth harmonic of the C and the fourth harmonic of the E beat at a frequency of approximately 10Hz. (The harmonics will beat at higher or lower frequencies as the pitches are transposed up or down.) The weaker tenth and eighth harmonics will beat at approximately 20Hz. The difference tones further complicate the picture. The first order difference tone (f2 – f1) is 68Hz, closer to C# than C. The second order difference tone (2f1 – f2) is 193.65Hz, a very flat G. The third order difference tone (3f1 – 2f2) is 125.6Hz, about a third-tone above B. None of these difference tones, if present, reinforce the identities of either of the tones that comprise the interval or any other closely related tone. The quality of this interval, which is accepted by most listeners as one of the most important consonances in Western music, is murky and ambiguous when compared to the just 5:4. The minor third and the major and minor sixths yield similar results. Hence, 12TET is a very poor system for music that requires consonant thirds or triads (which is the purpose for which it is commonly used). One would get even worse results in comparing the just harmonic seventh (7:4) with the 12TET minor seventh, but this does not seem like a fair comparison, since 12TET was never intended to approximate septimal, just intervals.

Composers and theorists working in just intonation frequently classify intervals, scales, and chords in terms of prime numbers and “prime limits.” A prime number is an integer (positive whole number) that is evenly divisible only by itself and one. The prime numbers that have an obvious role in just intonation are 2, 3, 5, 7, 11, and 13, though some composers have used much higher primes. The highest prime number used as a factor in the ratios that comprise a scale or gamut is called its “prime limit.” Why are prime numbers important? Each prime number used in a just tuning spawns a family of intervals that can be generated by no other method. The first prime, 2, generates the octave and its multiples: Multiply or divide any frequency by 2 and powers of 2 as many times as you want and all you’ll get are octaves above or below your starting pitch. The octave is necessary, but it is just an empty frame. To add musically useful tones, you must use other prime numbers. The second prime, 3, in combination with 2, generates the perfect fifth (3:2) and perfect fourth (4:3). Making chains of fifths and/or fourths and “folding” them back into an octave (one of the oldest known tuning methods) can generate melodically useful scales, known as 3-limit or Pythagorean scales, but such scales lack consonant thirds and sixths and hence, consonant triads. To create consonant thirds and sixths requires the prime number 5. Combined with the previous two primes, this yields the major third (5:4), minor sixth (8:5), minor third (6:5), and major sixth (5:3). 5-limit just intonation is the closest to the conventional Western vision of harmony and melody, though with triads that are truly consonant and an expanded intervallic palette. The prime 7 adds three more consonant intervals, the subminor third (7:6), the septimal tritone (7:5), and the harmonic or subminor seventh (7:4), which lie outside of conventional Western music theory and practice. The next two primes, 11 and 13, yield intervals that are not easily classified, but are, in many cases, as remote as possible from the intervals of 12TET. Prime 11, in particular, yields melodic intervals such as neutral seconds and neutral thirds, which are more typical of Arabic, Persian, and Turkish scales.

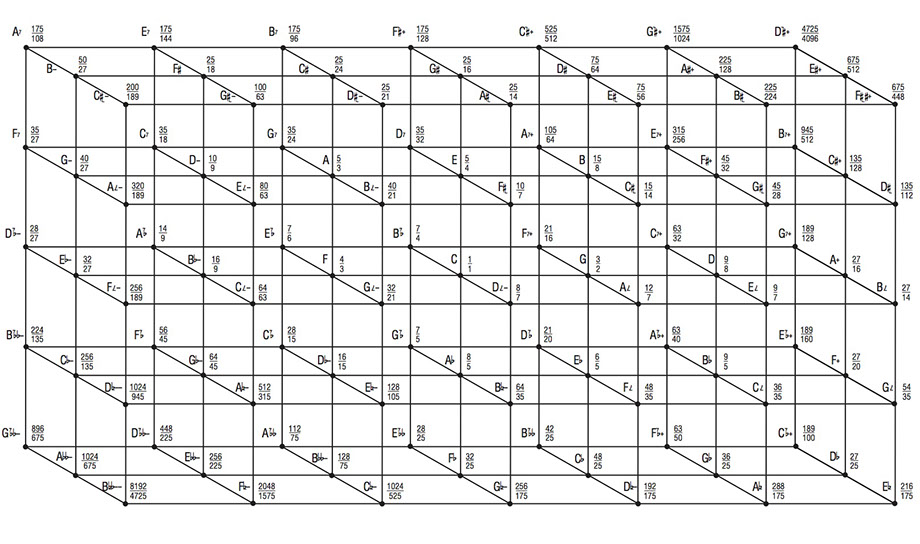
It is often useful to represent just tunings in the form of a lattice, such as that in Figure 5. Such a lattice normally uses one axis for each prime factor (2 is usually omitted, because each pitch is assumed to exist in all octaves). Unless one wants to draw hypercubes and the like, this technique is limited to tunings with three prime factors, excluding 2. The lattice in Figure 5 shows a portion of 7-limit tonal space centered (arbitrarily) around C 1/1. The horizontal axis represents the perfect fourth/fifth (prime 3), the vertical axis represents the major third/minor sixth (prime 5), and the diagonal axis represents the subminor seventh/supermajor second (prime 7).

So far, we have been talking about the properties of musical intervals in isolation. This is much like talking about the properties of paint squeezed from a tube onto a palette. Musical intervals or painter’s colors are not without aesthetic affect when encountered in isolation like this, but it requires the work of a skilled painter or composer to use these materials in a way that reveals their true significance.

My first encounter with JI was via the music of Harry Partch (1901–1974). While a student at the Chouinard Art Institute in Los Angeles in 1969, when I was first beginning to think of composing, I saw two films involving Partch’s music and instruments: Windsong and Music Studio, as part of a talk by Partch disciple Dean Drummond. Shortly thereafter, I purchased the Columbia LP The World of Harry Partch, which was one of the few commercial recordings of contemporary music in JI then available. At the time, I was more impressed by the timbres of Partch’s instruments, the textures of his music, the visual beauty of the instruments, and the general air of the strange and exotic hovering over it all. I did not understand anything about JI theory beyond the fact that Partch’s scale involved 43 tones and, of course, that this was not the conventional Western scale. For me, then, the initial experience of just intervals was indistinguishable from the experience of Partch’s music. My current opinion is that, whatever its musical value, Partch’s later music, such as I heard in 1969, is not the ideal introduction to JI. Whether one loves or hates Partch’s work (and it usually elicits strong responses), much of it does not show the intervals of JI to good advantage, being dominated by rapid percussion figuration, complex inharmonic timbers, and microtonal glissandi. A simple consonance or consonant chord, sustained and unadorned, is seldom heard.

It was not until about five years later that I had a second and more revelatory encounter with JI. In the summer of 1975, I enrolled in a class called “Intonation in World Music,” presented by Lou Harrison at the Center for World Music in Berkeley, California. In this course, I learned the fundamentals of JI, its relation to various musical cultures, and how to work with musical ratios. Equally important, I had the experience of JI in conjunction with a very different musical aesthetic. At the time, Lou and Bill Colvig were building their first American gamelan, later known as “Old Granddad” (the instruments used in the Suite for Violin and American Gamelan and La Koro Sutro). Students were invited to perform in a concert on these instruments at the end of the term and several also composed for the ensemble (I did not). Old Granddad was tuned in a straightforward just D-major scale, about as different from Partch’s scale as possible in the realm of JI. Several of the pieces presented were in a minimalist/proceduralist style, a compositional practice that interested me at that time. The simple intervals of 5-limit JI, heard in that context, were stunningly beautiful. That experience changed my life. I came away from that class and concert with both the tools necessary to understand JI and the germ of a compositional and instrument-building program that culminated in the creation of Other Music’s American Gamelan in 1977–78.⁴

What is the point of this personal reminiscence? When I first became aware of JI and decided that I wanted to incorporate it into my music, examples of recorded music in JI were rare, and opportunities to hear it in performance were rarer. Books and articles on the subject were few in number and often difficult to understand. The second edition of The Harvard Dictionary of Music (1969) described JI as “practically useless.” And in order to work in JI, it was necessary to build or modify instruments, as Partch and, to a lesser extent, Harrison and Colvig had done, or to learn how to play in JI on an existing instrument (with few models, if any, to emulate). Things have changed enormously in the intervening 43 years. The first revolution came with the introduction of commercial synthesizers with user programmable tuning. The first of these was the Sequential Prophet V, a digital/analog hybrid. Version 3 of this instrument, produced in the early 1980s, had the ability to store 12-tone tunings in patch memory. The Yamaha DX7 II digital FM synthesizer, introduced in 1983, brought this capability to a truly mass-market instrument, and many others followed. Anyone with an appropriate synth and a MIDI sequencer could begin exploring JI.⁵ It was these developments that motivated me and my colleagues to found The Just Intonation Network in 1984, so that those following this path would have access to accurate and understandable information.

The second revolution was marked by the creation of the Scala file format for representing tunings and the availability of “soft” instruments (“plug-ins”) that work in conjunction with a digital audio work station (DAW) or MIDI sequencer. Many available soft instruments support the Scala format, making it even simpler for the novice microtonalist to explore and compare tunings on a properly equipped computer. An example of a Scala file for Lou Harrison’s Incidental Music for Corneille’s Cinna (1956) is shown in Figure 6.⁶ Even if one ultimately decides to commit to composing for acoustic instruments, these tools are invaluable for exploring and composing in different tunings. The advent of downloadable and streaming music services, though a bane to composers’ and musicians’ finances, allows the student to easily hear examples of almost style of music imaginable by almost any composer. Thus, the paths now open to the beginner are both more numerous and less laborious than those I encountered in the 1970s.

There is no simple answer to the question “how do I go about composing in JI?” once you have acquired the basic resources needed to begin. There is no manual or course that will tell you how to do it. It is a question that individual composers must answer for themselves, depending on their musical taste and aesthetic preferences, and on how the music is ultimately to be performed. Lou Harrison, in his Music Primer, made a useful distinction:

After only a brief study of intervals it becomes clear that there are two ways of composing with them: 1) arranging them in a fixed mode, or gamut, & then composing within that structure. This is the Strict Style, & is the vastly predominant world method. However, another way is possible—2) to freely assemble, or compose, with whatever intervals one feels that he needs as he goes along. This is the Free Style…⁷

I would add that there is a “middle way” (with apologies to Buddhists): begin with a fixed scale or mode and then add pitches as required for harmony, counterpoint, transposition, modulation, and so on. This is the approach I use in much of my work. Additionally, pieces composed within a sufficiently large gamut, such as Partch’s 43-tone scale or Ben Johnston’s hyperchromatic scales, may be indistinguishable from “free style” compositions.

The Strict Style, in addition to being the “vastly predominant world method,” is the method used in many works by composers including Lou Harrison himself, Terry Riley, La Monte Young, Michael Harrison, and many others. This approach is more or less necessary if one intends to compose for a fixed-pitch instrument, such as a retuned piano or harpsichord or a refretted guitar, or an ensemble such as the Harrison/Colvig American gamelan. (Composing in the free style is a subject for advanced students, and is beyond the scope of this article.) If you have some experience with composition, you already have some idea of what sorts of scales, modes, and harmonic progression interest you and what their expressive properties are. Try mapping different versions of these figures onto a JI lattice like that in Figure 5. (Learn to construct such lattices for yourself; they’re a vital tool for understanding JI.) You will discover that there are many different versions of familiar resources such as pentatonic or diatonic scales. In 12TET, there is only one whole tone and one semitone, which can be arranged in a limited number of ways to construct five- or seven-tone scales. (There are only eleven unique intervals smaller than an octave in 12TET, though they may, in some cases, be called by different names.) In contrast, JI offers a much larger variety of such intervals (see Table 3), which can be used in constructing scales that are at once familiar and novel. Different versions of familiar scales will have different expressive properties and tonal centricities. Once one has chosen a mode or gamut, what then? Take time to familiarize yourself with all of the tones and the intervals that connect them. By this I mean familiar both aurally and computationally. Which intervals feel stable and which are in need of resolution? What melodic or harmonic figures lead to or away from the stable intervals?

When composing in 12TET, you never need ask yourself, “which Bb do I want here?” or “am I sure that I want a G# here rather than an Ab?” (and which G# or Ab?). In JI, such questions are meaningful and often critical. Referring to the lattice in Figure 5, you will see that there are three varieties or “flavors” of “Bb” in close proximity to C 1/1. B7b 7/4 is the harmonic seventh of C. Bb– 16/9 is a perfect fifth below F 4/3 and a 9:8 whole tone below C. Bb 9/5 is a minor third above G 3/2 and a smaller 10:9 whole tone below C. Any of these tones could be used melodically in relation to C, though with different effects. Harmonically, their uses are quite distinct. B7b 7/4 can be used to form a consonant dominant-seventh type chord with C, E, and G or a subminor triad with G and D. Bb 9/5 is the minor third of a minor triad on G 3/2. Bb– 16/9 is the root of a triad including D– 10/9 and F 4/3. All of these tones also perform other roles in tonalities more distant from C 1/1. One need not look far on the lattice to see many other pairs of tones near C 1/1 that are represented by a single tone in 12TET, such as D 9/8 and D– 10/9 or A 5/3 and A+ 27/16 or C 1/1 and C7+ 63/32. Recognizing such distinctions and understanding their melodic and harmonic implications is an essential aspect of understanding and working with just intonation.

It is much easier to explain how not to compose in JI: Write a piece as you typically do in 12TET and then try to impose a just tuning after the fact. This will cause you no end of trouble.