Whenever there are at least two pitches, something exists that we can call “harmony”—their relationship. There are infinite ways to tune a pair of pitches, and choosing how to do so invokes many factors—cultural, social, economic, mechanical, historical, political. As such, in respectful (and minor) disagreement with the famous dictum of my lifelong friend, colleague, and mentor, Lou Harrison, I do not think that “just intonation is [necessarily] the best intonation.” There are strong acoustical and cognitive arguments in support of Harrison’s claim, but from a composer’s perspective, it seems to me that the choice of how to tune depends on what one is trying to do, what is meant by “best,” and, ironically, on what is meant by “just intonation.” On the other hand, just as ironically, I have worked in extended rational tunings (“just intonation”) for close to 50 years.

All tuning systems—equal, well-tempered, just, octave- and non-octave based, and so on—have their own virtues and restrictions. Like one’s children, friends, teachers, students, and life experiences, each is complex, fascinating, and fecund in its own ways. Even the oft-maligned 12TET (“12 tone equal temperament”) offers the advantage of an extremely rigid, disciplined, paratactical paucity—only 12 pitch classes, each of which represents an infinite number of possible tunings!—that has somehow driven the evolution of European-based musical styles for several centuries, resulting in an enormous and incredibly varied amount of music, and perhaps culminating (but not ending) in Schoenberg’s declaration of the “emancipation of the dissonance.” Given its legacy, it’s hard to, in good faith, call 12TET a limitation.

Many 20th-century musicians—such as Hába, Carillo, Ives, Wysnegradski, Fokker—embraced the concept of octave-based equal temperament and devised greater (than 12) divisions of the octave in order to include representations of smaller pitch intervals, often in the service of approximating important just, or rational, intervals, such as the “good m7th” of 31TET. Two important composers in the field of experimental intonation have exploited 72TET in order to approximate complex rational tunings that may be played by conventional instruments: Ezra Sims, in the design of his 72-note scale from which smaller (generally 18-note) modes are selected; and James Tenney, whose Changes (1985), a large piece for 6 harps retuned in 1/6th tones, uses the resultant 72TET scale to closely approximate a large set of ratios, some extremely complex.

The exploration of rational tunings is an old and cross-cultural endeavor. Rationality, I believe, influences all tunings¹, but in many different ways. Simple whole number ratios make sense cognitively, acoustically, logically, and logistically. They happen even without us having to do much. The “simpler” the ratio (the smaller the number of prime factors, the smaller the magnitude of those factors and their exponents) the easier a frequency relationship is to generate, and perhaps to perceive. Small whole number ratios are (perhaps tautologically) more “consonant,” whether considered from an acoustical, mathematical, perceptual, or even a cultural perspective. Our brains seem to have evolved to favor ratiometric over arithmetic perceptions of difference, so the simpler the ratio the better it is for most tasks. It’s easier to slice a pizza or divide a pile of marbles into 2 or 3 parts than into 7 or 11 parts, much less say “that pile has about twice as many stones in it” rather than “that pile has 20 stones, the other 43.” This argues, musically and acoustically, for some measure of ratiometric simplicity, often in the form of harmonic distance (HD) functions.² Three well-known ones are Euler’s GS function and the harmonicity functions of Tenney³ and Clarence Barlow. Each is an evaluation of harmonic complexity, and in some sense, cognitive load. Measures of harmonic distance, in a way, are not all that dissimilar from Schenker-ism or Schoenberg’s ideas in Structural Functions of Harmony. These formal measures, including some of my own versions, play an important structural role in my work, especially in those pieces written primarily by software (some examples are Jargon⁴; 85 Chords (“The Historical Tuning Problem”) from Songs and Toods⁵); and Yitgadal⁶).

Like the music of James Tenney, Ezra Sims, Lou Harrison, Ben Johnston (to cite just a very few examples), my work often deals with what Johnston called “extended just intonation,” but which might also be called extended rational tunings. The possibility of a new and highly structured set of pitch relationships outside of 12TET (whose hegemony is relatively recent, historically) provides a huge resource of new harmonic and formal possibilities. Music that emanates from a compositional commitment to rationally tuned ratios is as heterogeneous as music in 12TET or any other tuning system.

My compositional (and theoretical) work has consistently explored rational tunings since the early 1970s. In retrospect, I can loosely identify a few common areas that have interested me:

The use of conventional, unaltered instruments to produce extended just intonation ideas⁷;

The avoidance of ideas of “scale” or “mode” in favor of a free, complex harmonic fabric;

The harmonic series, and more, the use of multiple harmonic series, as a fundamental harmonic source (sometimes, just implied by 12TET, such as the twooaytoods for piano);

The idea of what Lou Harrison called “free style” tuning^8,9, and which I’ve called “paratactical” or “adaptive” tunings, where things are tuned “on the fly” or in relation to other pitches produced in the same manner (a way, in fact, of avoiding ideas of scale and mode). Much of this work has involved real-time computer software.^10,11;

Most importantly, the use of harmony as primary determinant of form, in which harmonic morphology may be even the sole such determinant;

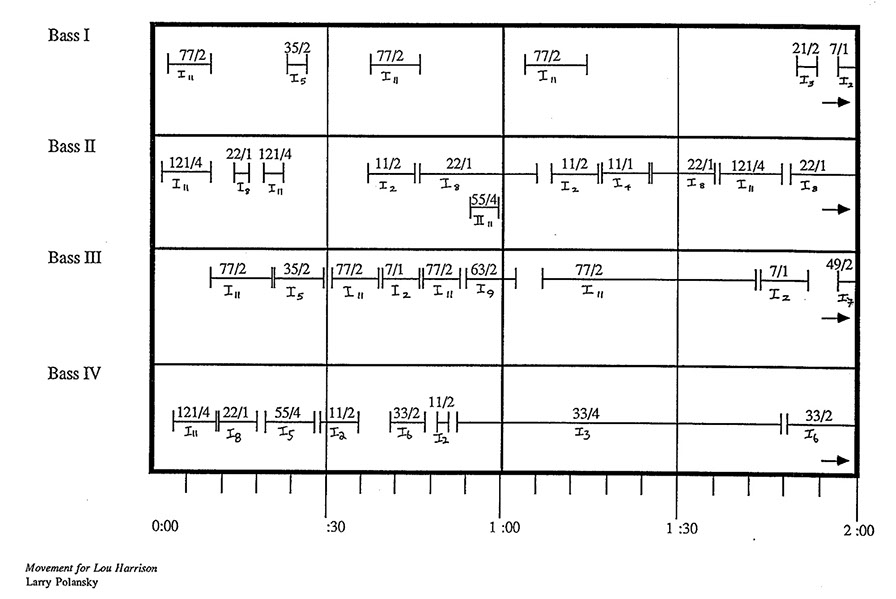
My earliest works, from the 1970s, are from the first category and include Movement for Lou Harrison (for just bass quartet)¹², Movement for Andréa Smith (for Just String Quartet)¹³, and Piano Study #5 (for just Fender Rhodes)^{14, 15}. Movement for Lou Harrison and Movement for Andréa Smith employ a technique borrowed from Quintext #5: Spectra for Harry Partch, the final piece of James Tenney’s pioneering Quintext (Five Textures for String Quartet and Bass), (1972)¹⁶, in which conventional string instruments are retuned to a set of rational ratios, and played by sounding natural harmonics. This allows for the production of a large number of complex ratios on the different open string fundamentals. Players need not be conversant in rational tuning systems and their arithmetic in order to perform the piece—the acoustics of the instruments take care of that. One disadvantage is that octaves tend to get quite high, and the higher the harmonic, the more difficult it is to produce. I also used this instrumental technique in much later pieces like the above-mentioned Jargon, Yitgadal (2005), melodically in the String Quartet in Three Movements (2010), and in a slightly different way in Four Voice Canon #17 (“Guitar Canon”)¹⁷.

In Movement for Lou Harrison, the basses are retuned so as to obtain a maximal variety of ratios produced as natural harmonics. The piece has a simple form. It goes from maximal dissonance (high harmonics, like the 11th on the various strings) to maximal consonance (low harmonics). It’s a kind of chorale, whose harmonic form corresponds to the movement from high to low primes.

Movement for Andréa Smith (“My Funny Valentine” for Just String Quartet), a four minute, two-part piece for two violins and two violas, was written for a dance by the eponymous choreographer. In similar fashion, the 16 strings are tuned to different small number ratios, and only natural harmonics are sounded. The piece is quiet, slow, and ethereal, exploring the possibilities of harmonies based on the ramifications of the tunings. The first part “quotes” the tune “My Funny Valentine,” playing with the song’s melody and its emblematic minor 3rd and major 7th intervals. The second section “quotes” an intervallically similar chord, the “theme” of Carl Ruggles’s “Angels” (a M7th chord with both a minor and major 3rd).

Notation is always a question with non-12TET pieces, and in these pieces, and since, I have generally employed some form of tablature, giving the number of the string (Roman) and the harmonic on the string (Arabic), along with the resultant pitch and its cents deviation from nearest 12TET neighbor (the latter an indication more for the composer than the performer). In this way, both of those pieces were essentially sight-readable. Occasionally, in other pieces, performers have requested a more conventional “nodal” notation, indicating string number and the location (placement) of the finger on the string. As a composer, I’m not particularly fond of this notation, which seems antiquated and, in a way, to not fully take advantage of a musician’s intelligence (that is, to know how to sound a specific harmonic pitch on given string). However, sometimes the nodal notation has been useful in facilitating performances of pieces for larger ensembles (like Jargon and Yitgadal), and with limited rehearsal time.

Piano Study #5 has had a long, interesting, and well-documented history, culminating in a new recording by the composer and pianist Andrew Smith, who is the first person other than myself to play it. Performing it requires a knowledge of tuning, a Rhodes piano, and the willingness and skill to retune it (not to mention carry it!). The tuning is non-octave replicating, based on C, with a variety of minor 2nds to the tonic, and a number of 5ths and triads built on higher primes like 7, 11, and 13. It was inspired by a request from trumpet player Jon Hassell, who used it as an accompaniment on his Vernal Equinox LP (Lovely Music Records, 1978). It became a solo piece for me after that, which I performed several times and eventually recorded. The score consists of the tuning and some simple directions, and is essentially a directed improvisation. The performer picks a song to use as a source, and structures the improvisation in the context of a harmonic movement from low to high prime-based and back over the course of the piece.

Tuning for Piano Study #5

Octaves 1 & 2: 1/1, 21/20, 9/8, 6/5, 5/4, 4/3, 7/5, 3/2, 8/5, 5/3, 7/4, 15/8
Octave 3: 1/1, 33/32, 9/8, 6/5, 5/4, 21/16, 11/8, 3/2, 8/5, 13/8, 7/4, 15/8
Octave 4: 1/1, 21/20, 9/8, 7/6, 5/4, 4/3, 11/8, 3/2, 8/5, 27/16, 7/4, 15/8

Over the years I have written many other pieces for conventional instruments (including Yitgadal, V’y’aal, 3 Cello Tunes (1998), for jim, ben and lou, Piker (for solo piccolo) (1998), 8 fermentations (on a sketch by Charles Dodge) (for two electric guitars) (2017) in which conventional instruments are unconventionally but specifically tuned. My compositional focus is to allow tuning possibilities to generate and become the form and structure of the work. I generally avoid the idea of tuning as exoticism—some kind of “new sound”—as well as the notion that different tunings have different affective emotional or connotative affects. I am more interested in formal and structural processes than dramatic and cosmetic ones. Most of my pieces in just intonation, with a few exceptions (such as Songs and Toods; for jim, ben and lou; Another You (for solo harp) (1980), Will You Miss Me (1978)) are more vertical than linear, the form in time is some particular harmonic evolution. Unlike the extraordinary work of Ezra Sims, Ben Johnston, and Lou Harrison—all of whom have used extended tunings to create new scalar resources, and have written beautiful, rich, complex, and virtuosic work in that domain—my own music outside of 12TET has generally not been focused on melody. I have often eschewed the idea of a hierarchical scale in favor of an acoustically derived and heterarchical gamut or field. A tuning’s numerical structure evinces its harmonic possibilities, and those possibilities generate the idea, form, and content of the piece. A good, but exceptional example is Will You Miss Me¹⁸, written for my own voice and Harrison/Colvig transfer harp, which I recently revived for performance in honor of Lou Harrison’s 100th birthday. That piece was written as an explicit and deeply felt homage to Ben Johnston and his music.

Quite often in my work, the harmonic series has been the form and the content of the piece. Composers throughout history have often acknowledged the harmonic series as a font for harmony, and indeed, 12TET itself. Schoenberg even used it to explain the genesis of 12ET pitches in his essay on 12-tone music (in Style and Idea). A more home-grown tradition, for me, originates in Cowell’s work in the “rhythmicon” (and “rhythmicana”), and finds its later extraordinary expression in James Tenney’s music. Tenney treats the harmonic series as an acoustical, mathematical, philosophical, and aesthetic font, resulting in some of his finest works, such as Spectral CANON for CONLON Nancarrow. In that piece, and others, the harmonic series is the temporal, harmonic, and formal structure.

Psaltery (for Lou Harrison) (1978)¹⁹, uses a few notes played on a small, hand-held bowed psaltery, a large number of pitch-shifted tape loops, and a classic tape-music studio to create a continuous modulation between three harmonic series (up to the 17th harmonic), related by their fundamentals as 1-3-5 (and back to 1). Pitches from the next series gradually replace pitches from the previous (by a simple method), so that a dense, modulatory chord is produced. New pitches enter from their highest harmonic down in an order related to their harmonic complexity (17, 13, 11, 14, 7, 15, 10, 5, 9, 12, 6, 3, 16, 8, 4, 2, 1), in what I call Psaltery-order (or “reverse Psaltery-order”)

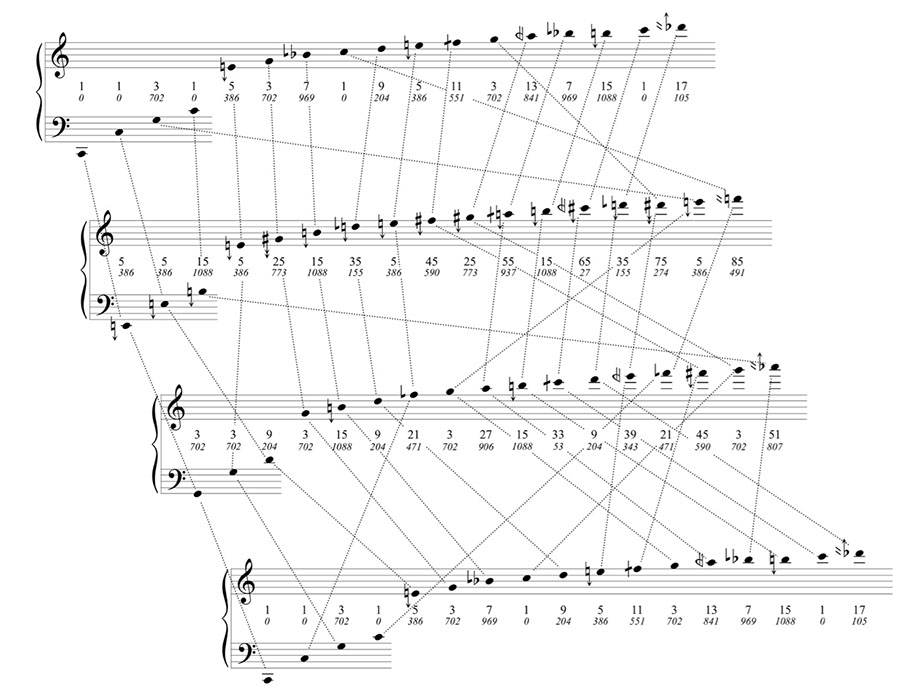
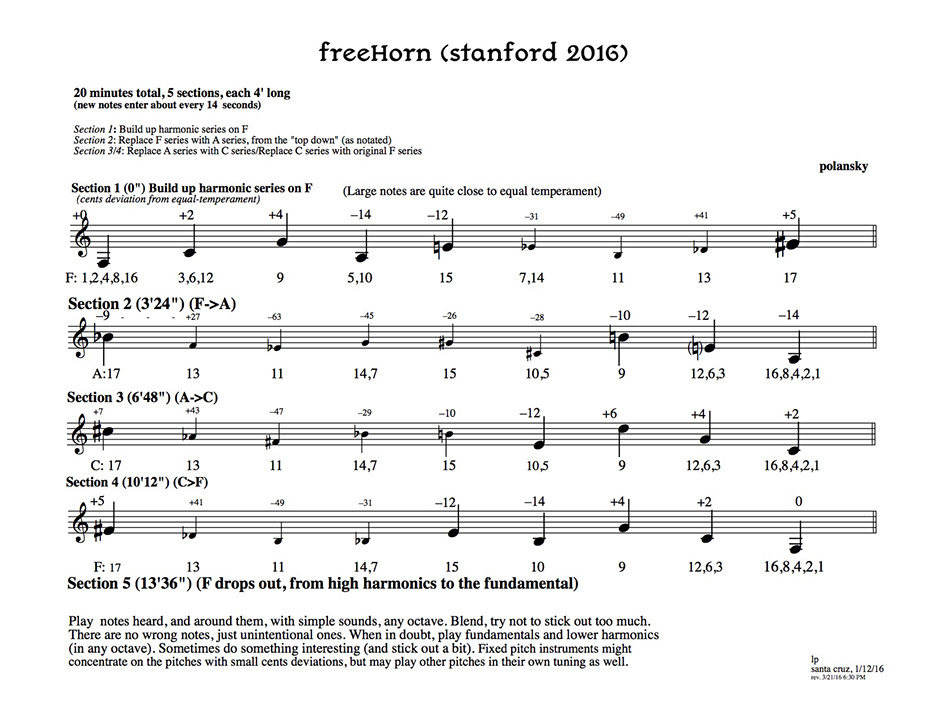
Psaltery spawned a number of “heirs” over many years, including Glass²⁰, Horn²¹, Choir (Empi’s Solo)²², and ultimately freeHorn²³ and its many versions. The formal ideas of Psaltery have also found their way more locally into other pieces (for example, the first of the three pieces of for jim, ben and lou, called “Preamble”)²⁴. In the choral work 3 New Hampshire Songs²⁵ each of the songs is generated entirely by a different compositional strategy for elucidating the harmonic series, motivated by the idiosyncratic state-specific texts. freeHorn, stand-alone computer software, written in Java/JSyn by myself, Phil Burk, and Mike Winter, generalizes the ideas of Psaltery. The software can be used in performance with live instruments, or in any way. freeHorn has been performed often by a wide variety of ensembles, with varying musical aesthetics.

Lou Harrison’s idea of “free style” tunings—tunings that are not the result of a pre-defined scale but are tuned “on the fly” to some other instrument or in linear fashion—is, in my opinion, one of the most radical, interesting, and visionary musical ideas of the 20th century. For practical reasons, Harrison only used this idea in a few pieces—including Simfony in Free Style (1955), At the Tomb of Charles Ives (1963), and A Phrase for Arion’s Leap (1974). Only the last of those, “... Arion’s Leap,” was performed successfully in his lifetime. While written in free-style, because of its notation and instrumentation, unlike the other pieces, it doesn’t require the performers to tune in real-time performance. The idea of free-style as a compositional rather than performance idea is beautifully illustrated by some of the works of James Tenney, in which pitches are determined by a highly controlled note-by-note exploration of harmonic space. Tenney’s final work, Arbor Vitae (for string quartet) (2006), completed by Mike Winter, is one of the finest examples of free-style composition in extended just intonation.

The idea that the tuning terrain is navigable in real time, involving no fixed, limited set of choices, has always been important to me, especially with regard to my work in live, interactive intelligent computer music systems (from the 1980s on). The idea of an “adaptive tuning” (pioneered and suggested by the composer/engineer Harold Wagge in a seminal article in the journal 1/1)²⁶, was not only appropriate for, but facilitated by the idea that a computer has no problem tuning in real time, employing some musical intelligence, whether in response to external stimuli or not.

My work B’rey’sheet (1986)²⁷, for singer and live interactive computer, written in the computer language HMSL (Hierarchical Music Specification Language, written by Phil Burk, myself, and David Rosenboom at the Mills College Center for Contemporary Music), embodies Lou Harrison’s idea in a new technological realm. In B’rey’sheet, the (mostly pentatonic) conventional cantillation of the first 17 verses of the Hebrew Torah is sung in a simple 7-limit just scale. The computer “listens” and “plays along,” using any pitch it likes from the available “dimensionality” of the pitch space. That dimensionality decreases from 17 (the possibility of all pitches containing all factors of 1–17 in the numerator and/or denominator, with all possible exponents) to 1 (unison with the voice). It progresses slowly (along with the text) from a huge, chaotic harmonic space to the simplest, smallest one possible. There are parallel rhythmic and timbral algorithms in the computer software as well. The computer decides what pitch(es) to play based on the vocal input and its own current notion of the harmonic universe. The piece is performed live, always different, often surprising (to me). The computer performer’s sole task is to tell the computer which verse it’s in (and to ride gain!).

Humans can also retune and adapt, in real time. My guitar duet II-V-I (1996)²⁸, first written for a somewhat impromptu performance in New York City by myself and Nick Didkovsky, simply asks the guitarists to retune their strings over time to harmonics (subsets of 1–17) of fundamentals related as the “chord changes” II,V,I, while playing continuously. In other words, in one version (there are a number of different versions), the first series is based on D, the second series on G, the third on C. Each guitar tunes to different harmonics of the target fundamental. In this way the 12 strings, at any given time sound some significant portion (though not in the correct octaves) of the three fundamentals’ harmonics. There are also suggestions about how to articulate the arrival on a given series, and the restriction that only octaves, P5ths and 4ths, open strings, and harmonics be played (so as to keep all pitches in the realm of rational tuning).

After Nick and I premiered the piece on a few hours of rehearsal (a testament to Nick’s extraordinary musical intelligence and guitar chops), I’ve played it many times with other guitarists, and it has been also been performed often without me. I use a similar, perhaps slightly more theatrical, idea in Preamble (for Jim Tenney) from for jim, ben and lou²⁴, a set of three pieces for guitar, harp, and percussion. The harp is retuned to a complex just intonation (the tuning is different between the first piece and the other two). In Preamble, which follows a "Psaltery/ii-v-i (-ish)" form, the percussionist continuously retunes the guitar, in performance, between different harmonic series tunings (an idea inspired by both Lou Harrison’s free style and a Smothers Brothers’ comedy routine) over the course of the piece, while the guitarist and harpist play a difficult and rhythmically complex score.

I’d like to thank Nate Wooley for requesting this essay, and Amy Beal for valuable editing and advice.